就是調查所有可能性並從中找出解答的方法。(深度優先及廣度搜優先)
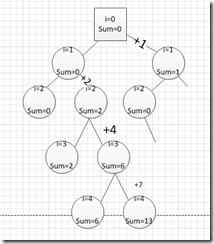
- 遞迴函式
- 在函式中再次呼叫同一個函式。在遞迴函式中,必定要有一個條件讓函式能停下。
- int fib(int n)
- if(n<=0) return n;
- else
- return fib(n-1)+fib(n-2);
- 在遞迴函式中,可將問題去將其數值存下。來加速其演算法速度。
- int memo[MAX_N+1];
- int fib(int n)
- if(n<=1) return n;
- if(memo[n]!=0) return memo[n];
- else return memo[n]=fib(n-1)+fib(n-2);
- 堆疊(stack)
- 使用pop and push
- 為FILO
- 佇列(queue)
- FIFO
深度優先搜尋法(DFS:depth first search)。從某種狀態開始讓將態遷移,若無法遷移則回到上一狀態搜找其它解答
(如數獨,先隨便決定格子的值,再繼續決定其它格子的值,不斷地重複此過程,如果無法抵達解答話,就回到上一步。)
範例: 提供整數a1,a2,..., an。請判斷從中選擇幾個數值的 提供整數a1,a2,..., an。請判斷從中選擇幾個數值的和能否剛好等於K。
(限制: 1<n<20. -10^8<ai<10^8, -10^8<k<10^8)
輸入: n=4; a={1,2,4,7}; k=13
輸出: yes 13=2+4+7
先從a1開始依序決定是否加上該值, 當n個全者決定好之後就判斷是等於k。由於狀態數約為2^n+1,所以時間複雜度會是O(2^n)。
1: #include <stdio.h>
2: #include <stdlib.h>
3: #include <stdbool.h>
4: #define MAX_N 100
5: int a[MAX_N]={1,2,4,7};
6: int n,k;
7: 8: bool dfs(int i,int sum){
9: //決定好n個值之後,判斷其和是為等於k並傳回結果.
10: if(i==n) return sum==k;
11: 12: //不使用a[i]的情況
13: if(dfs(i+1,sum)) return true;
14: 15: //使用a[i]的情況
16: if(dfs(i+1,sum+a[i])) return true;
17: 18: //other
19: return false;
20: 21: }22: void solve()
23: {24: if(dfs(0,0)) printf("yes \n");
25: else printf("no\n");
26: } 27: 28: int main()
29: {30: float fin;
31: //fprintf(STdout,"please input the fin(Osc)\n");
32: //fscanf(stdin,"%f",&fin);
33: n=4; 34: 35: k=13; 36: solve(); 37: 38: system("PAUSE");
39: return 0;
40: }而我所遇到的問題,則是輸入
Pllout=213Mhz, Fin=12Mhz,range=+-2.
213=12*176*/5/2=211.2
廣度優先搜尋(BFS,Breadth-First Search)。同深度優先搜尋,都是從某個狀態開始搜尋所有可抵達的狀態。與深度優先搜尋不同的是搜尋順序,廣度優先是從接近初始狀態的狀態開始搜尋。也就是依[剛開始的狀態->至少一次遷移可抵達的所有狀態->至少二次...]。
特別的是,在DFS中,不多次通過相同的狀態是不會包含在演算法中; 在廣度插尋中,將相同的狀態只通過一次的處理大抵上都包含在演算法中,時間只有O(狀態數X遷移方式)
DFS是使用堆疊,而BFS則是佇列。一開始先將初始狀態放入佇列中,然後再從佇列中取出狀態,並將該處能遷移的所有宋訪問的狀態放入佇列,重複上述步驟,直到佇列為空或找到解。
Q.有一大小為NXM的迷官。每回合都能往相鄰的上下左右四方移動。請計算從起點到終點需多少回合數。
限制: N,M <=100
1: #include <iostream>
2: #include <queue>
3: #include <cstdio>
4: 5: #define MAX_N 10
6: #define MAX_M 10
7: //#define INF 256
8: using namespace std;
9: 10: const int INF=100000000;
11: typedef pair<int,int> P;
12: char maz[MAX_N][MAX_M+1]=
13: {14: {'#','S','#','#','#','#','#','#','.','#'},
15: {'.','.','.','.','.','.','#','.','.','#'},
16: {'.','#','.','#','#','.','#','#','.','#'},
17: {'.','#','.','.','.','.','.','.','.','.'},
18: {'#','#','.','#','#','.','#','#','#','#'},
19: {'.','.','.','.','#','.','.','.','.','#'},
20: {'.','#','#','#','#','#','#','#','.','#'},
21: {'.','.','.','.','#','.','.','.','.','.'},
22: {'.','#','#','#','#','.','#','#','#','.'},
23: {'.','.','.','.','#','.','.','.','G','#'}
24: };25: int N=10,M=10;
26: int sx=0,sy=1;
27: int gx=9,gy=8;
28: int d[MAX_N][MAX_M];
29: int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
30: 31: int bfs()
32: { 33: queue<P> que;34: //以INF初始化所有點
35: for(int i=0;i<N;i++)
36: for(int j=0;j<M;j++)
37: d[i][j]=INF;38: //把始點放入佇列中,並將此點的距離設為0
39: que.push(P(sx,sy)); 40: d[sx][sy]=0; 41: 42: //在佇列全空之前loop
43: while(que.size())
44: {45: //取出佇列的前端資料.
46: P p=que.front(); 47: que.pop();48: //若取出的狀態為終點則停
49: if(p.first==gx && p.second==gy)
50: break;
51: //以可移動的四個方向loop
52: for(int i=0;i<4;i++)
53: {54: //將移動後的設為nx,ny
55: int nx=p.first+dx[i],ny=p.second+dy[i];
56: //判斷是否可移與斷斷有訪問過(d[nx][ny]!=INF
57: if(0<=nx && nx<N && 0<=ny && ny<M && maz[nx][ny]!='#' && d[nx][ny]==INF){
58: //可移動的放入佇列,並確定該點的距離為到p的距離+1
59: que.push(P(nx,ny)); 60: d[nx][ny]=d[p.first][p.second]+1; 61: } 62: } 63: }64: return d[gx][gy];
65: } 66: 67: void solve(){
68: int res=bfs();
69: printf("%d\n",res);
70: 71: }72: int main()
73: {74: printf("Hello world!\n");
75: solve();76: return 0;
77: }
由於BFS會從較近的狀態開始,所以可以求出最短路線及最少步驟。BFS中只需管理用來表示是否有訪問過的旗標,就自會從較近那方開始。由於是迷官,所以求最矩離,所以其最短距離存在d[N][M]中。一開始以INF來初始化,故尚未低達的地方都是INF,以此完成旗標工作。
雖然到了終點就停止,但若是不停止搜尋並持續佇列完全為空,就能算出各個點的最短距離。(即最後找到的d是INF,則為無路徑)。
同檥會產生所有能抵達的狀態。但DFS會重複經過同樣的路徑時,則以BFS。但BFS用到queue,所以需與狀態同大小的memory.而DFS則會遞迴的最大深度memory。由於遞迴的深度通常不會大於狀態數,所以使用DFS比較不佔memory。還有一種反覆DFS(IDDFS,iterative deepening depth first search),先以DFS找,找不到時再加深度。
剪技:
完全搜尋法,是會搜尋所有狀態,而其time complox會隨解答的候選變多。
而在這情況下,快速化方法為剪技
"在DFS中",常有其不繼續也清楚沒有結果。在這種情況直接停止搜尋。